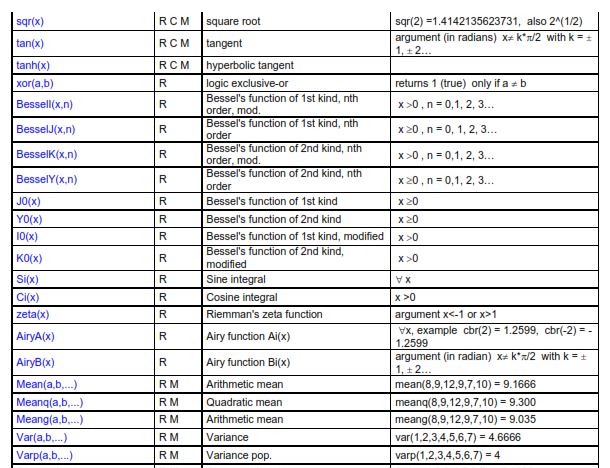
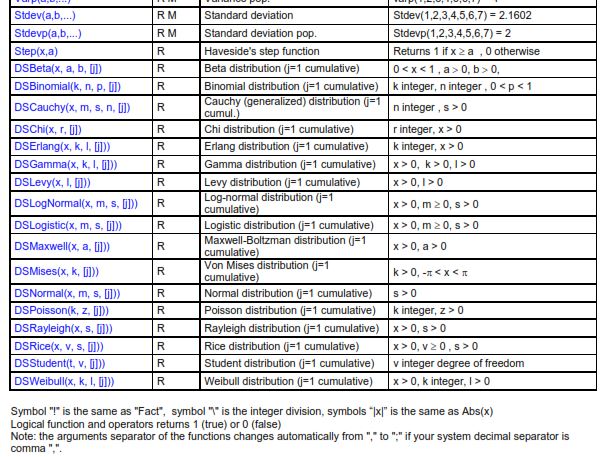
From
ANTHROPOLOGICAL MISCELLANEA
REGRESSION towards MEDIOCRITY in HEREDITARY STATURE
By FRANCIS GALTON, F.R.S. &C.
[WITH PLATES IX AND X.]
[Journal of the Anthropological Institute 15 (1886), 246–263.]
https://www.york.ac.uk/depts/maths/histstat/galton_reg.pdf
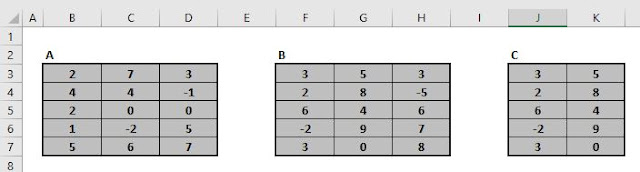
It is deduced from a large sheet on which I entered every
child's height, opposite to its mid-parental height, and in every case
each was entered to the nearest tenth of an inch. Then I counted
the number of entries in each square inch, and copied them out
as they appear in the table. The meaning of the table is best
understood by examples. Thus, out of a total of 928 children who
were born to the 205 mid- parents on my list, there were 18 of the
height of 69·2 inches (counting to the nearest inch), who were
born to mid-parents of the height of 70·5 inches (also counting to
the nearest inch). So again there were 25 children of 70·2 inches
born to mid-parents of 69·5 inches. I found it hard at first to
catch the full significance of the entries in the table, which had
curious relations that were very interesting to investigate. They
came out distinctly when I" smoothed" the entries by writing at
each intersection of a horizontal column with a vertical one, the
sum of the entries in the four adjacent squares, and using these to
work upon. I then noticed (see Plate X) that lines drawn through
entries of the same value formed a series of concentric and similar
ellipses. Their common centre lay at the intersection of the
vertical and horizontal lines, that corresponded to 68!- inches.
Their axes were similarly inclined. The points where each
ellipse in succession was touched by a horizontal tangent, lay in a
straight line inclined to the vertical in the ratio of 2/3; those where
they were touched by a vertical tangent lay in a straight line
inclined to the horizontal in the ration of 1/3. These ratios confirm
the values of average regression already obtained by a different
method, of 1/3 from mid-parent to offspring, and of 2/3 from offspring
to mid-parent, because it will be obvious on studying Plate X that
the point where each horizontal line in succession is touched by
an ellipse, the greatest value in that line must occur at the point
of contact. The same is true in respect to the vertical lines.
These and other relations were evidently a subject for mathe-
matical analysis and verification. They were all clearly dependent
on three elementary data, supposing the law of frequency of error
to be applicable throughout; these data being ( 1) the measure of
racial variability, whence that of the mid-parentages may be inferred
as has already been explained, (2) that of co-family variability
(counting the offspring of like mid-parentages as members of the
same co-family), and (3) the average ratio of regression. I noted
these values, and phrased the problem in abstract terms such as a
competent mathematician could deal with, disentangled from all
reference to heredity, and in that shape submitted it to Mr. J.
Hamilton Dickson, of St. Peter's College, Cambridge. I asked
him kindly to investigate for me the surface of frequency of error
that would result from these three data, and the various particulars
of its sections, one of which would form the ellipses to which I
have alluded.