Special functions: Gamma

All the elements presented are not warranted to be correct or free from defects. Please report any errors found to afstblogs@gmail.com Use also this address to get the Word and Excel files available concerning this subject

Gamma function

ERRATA
There is a minus sign missing in the formula for negative values as can be found by the values obtained in Maple. The formula presented returns a value with the opposite sign, that is, the value of -GAMMA(-a)
The Gamma(1/2) = sqrt(Pi)
21 DEZ 2017

1. Definition

Although the Gamma function can be defined in the complex plane we will only analyze its computation for real arguments.

Since the function is not defined for a=0, the leftmost a value used in the graph was a=1E+10.  

If the values of the function for any interval ]a,a+1 ] are known, it is possible possible to compute the values for the other intervals using the expression for a<>0.

Γ(a) = (a-1) Γ(a-1) 

2. Extension to negative values of a

However, it is quite common to see the gamma function evaluated for negative values as shown in the next figure that shows that it it is undefined for zero and negative integers.

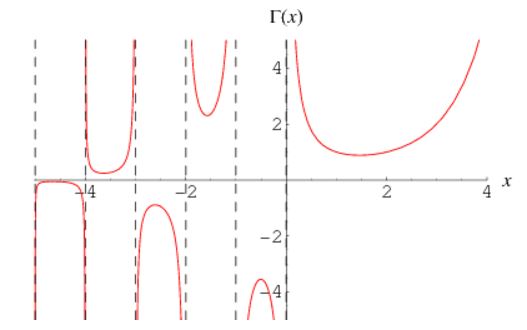
For a < 0 the function can be evaluated using the following reflection formula:

Excel functions and formulas

The function GAMMALN.PRECISE only works for a > 0.
The formulas if column H use the GAMMALN.PRECISE and the reflection formula to extend the computation to non-positive values. There is no convergence for zero and negative integers. 

DNC - Did not converge

C3: =EXP(GAMMALN.PRECISE(B3)) D3: =EXP(-1)/(GAMMA.DIST(1,B3,1,0))

H3: =IF(F3=0,"DNC",IF(F3<0,IF(F3=INT(F3),"DNC",PI()/ (ABS(F3)*SIN(PI()*ABS(F3))*EXP(GAMMALN.PRECISE(ABS(F3))))), EXP(GAMMALN.PRECISE(F3))))

One alternative formula for column H is to use a very large number instead of DNC in order to facilitate graphing the functions for the a values for which there is no convergence.

However, extending the computation for the entire real field implies non-convergence at the left and the right of zero and negative integers, requiring a solution difficult to implement using formulas in dynamic models.
The graph below was made using six series of paired data sets.

Excel user defined functions

Maple commands and Excel add-in

Maple commands and functions are case sensitive.

L3: =maple("GAMMA(&1)",K3)

'Gamma function Function xlGAMMA(a)   With WorksheetFunction     xlGAMMA = Exp(.GammaLn_Precise(a))   End With End Function

Matlab

>> gamma(0.5) ans =           1.77245385090552 >> a=(0.5:5),gamma(a)' >> a=(0.5:5)',GammaF=gamma(a) a =                        0.5                        1.5                        2.5                        3.5                        4.5 GammaF =           1.77245385090552          0.886226925452758           1.32934038817914           3.32335097044784           11.6317283965675