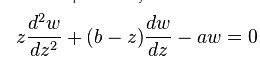All the elements presented are not warranted to be correct or free from defects.
Please report any errors found to afstblogs@gmail.com
|
Kummer's function of the first kind
This function is also presented as 1F1.
Kummer's function of the second kind
The function of the first kind will be used soon as part of the expression of the probability density functions of the noncentral Student's t and sample correlation distributions.
Excel formulas and user defined functions
The only function presented is the one for the firs kind contained in the function XN.xlam6056M add-in that is free and can be downloaded from http://www.bowdoin.edu/~rdelevie/excellaneous/.
It is not straightforward to compute this function without using VBA. In alternative the computation with Maple Excel add-in is presented. In future messages its use will be explained.
XNumbers60
'ATTENTION
'Const TOL# = 1.6 * Ten_16
'changed to
'Const TOL# = 1.6 * 1E-16
'return the M(a,b,z) Kummer confluent hypergeometric function of 1st kind
'it uses the serie expansion method
'
Function Kummer1(a, b, z)
Dim n&, kn#, PN#, dY#, y#, ua#
'Const TOL# = 1.6 * Ten_16
Const TOL# = 1.6 * 1E-16
kn = 1#: PN = 1#: y = 1#
'Kummer's transformation for negative value of z
If z < 0 Then ua = b - a Else ua = a
For n = 1 To 999
kn = kn * (ua + n - 1) / (b + n - 1)
PN = PN * Abs(z) / n
dY = kn * PN
y = y + dY
If Abs(dY) < TOL * Abs(y) Then Exit For
Next n
If n < 999 Then
If z < 0 Then y = y * Exp(z) 'Kummer's anti-transformation
Kummer1 = y
Else
Kummer1 = "?"
End If
End Function
|
Matlab
Matlab has not a function to compute this function, meaning that a user defied must be used. The one presented below is fromhttp://www.mathworks.com/matlabcentral/fileexchange/29766-confluent-hypergeometric-function/content/kummer.m
function f = kummer(a,b,x)
% This function estimates the Kummer function with the specified tolerance
% the generalized hypergeometric series, noted below. This solves Kummer's
% differential equation:
%
% x*g''(x) + (b - x)*g'(x) - a*g(x) = 0
% Default tolerance is tol = 1e-10. Feel free to change this as needed.
tol = 1e-10;
% Estimates the value by summing powers of the generalized hypergeometric
% series:
%
% sum(n=0-->Inf)[(a)_n*x^n/{(b)_n*n!}
%
% until the specified tolerance is acheived.
term = x*a/b;
f = 1 + term;
n = 1;
an = a;
bn = b;
nmin = 10;
while(n < nmin)||max(abs(term) > tol)
n = n + 1;
an = an + 1;
bn = bn + 1;
term = x.*term*an/bn/n;
f = f + term;
end
% VERSION INFORMATION
% v1 - Written to support only scalar inputs for x
% v2 - Changed to support column inputs for x by using the repmat
% command and using matrix multiplication to achieve the desired sum
%
% v3 - Credit goes to Ben Petschel for making this suggestion.
% The previous method of creating vectors for multiplication to
% produce the sum was replaced by a while loop that executes
% until a certain tolerance is achieved. My previous thinking
% was avoiding a loop would produce a code that would execute
% faster. Ben pointed out this is not necessarily true, and not
% true in this case. Not only does the while loop used execute
% faster for this calculation, but it is also more accurate.
end
|